利用Excel實作股利的複利利率計算

最近正在看《和巴菲特同步買進》，其中有提到巴菲特計算股利的複利利率，但當我用Excel計算時，卻發現巴菲特所計算的利率，與真實值有出入…

利用Excel實作

利用Excel實作股利的複利利率計算時，如果你用Google去搜尋時，得到的答案大多是採用Rate(nper, pmt, pv, fv, type, quess)這個函式去計算：

• nper 為付款總期數；


• pmt為每期應繳金額，因為是「付出」的錢，所以要加負號；


• pv是貸款總額；


• fv是期滿領回金額；


• type是指期初或期末付款，如果是期初付款，就填1；


• guess就是要猜測的值，若不填， 函式預設從0.1(10%)開始猜。

以一個實際的例子為例：假設你借了80000，每個月還9000，共還12期時，利用Rate這個函式：RATE(12, -9000, 80000)，就可以計算出0.0495的值，也就是4.95%的利率。

實際案例實作

以下是我正在研究的一檔股票「台汽電」(8926)的過去資料：

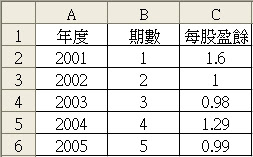
如果仍然使用Rate這個函式，是無法計算股利這類的利率，在我又花了好幾個小時研究Excel內其他計算複利的函式包括：Effect、Norminal、FVSchedule、FV、Geomean後，最後我發現如果只使用Excel所提供的這類函式，都無法計算出股利的複利利率。

另闢蹊徑

就在我遇到瓶頸時，我就想乾脆用手算好了，就寫了一個簡單的試算：假設5年內的績效是100%（成長一倍），那每年的複利公式就是：
(1+x)^5=2
(1+x)=5√2
x=(5√2)-1
原來，這可以使用Excel內計算√的函式POWER(number,power)：

• Number是底數。可以是任意的實數。


• Power是指數，即底數所要乘方的次數。

這樣就能算出利率x了。

利用Power函式計算股利的複利利率

我們繼續使用這個試算表，假設我在2001年除息前買進一股，假設5年的股利配的都是股票股利，然後在2005除息後賣出，這時計算股利利率的D6：
=POWER(((1+$C2*0.1)*(1+$C3*0.1)*(1+$C4*0.1)*(1+$C5*0.1)*(1+$C6*0.1)),(1/5))-1

最後可以算出5年以來的股票股利複利利率為0.1169，相當於11.69%。

倘若以巴菲特的公式來計算股利利率的E6：
=POWER(((1+$C6*0.1)),(1/5))-1

最後可以算出5年以來的股票股利複利利率為0.0191，相當於1.91%。

解釋巴菲特計算出來的值為何低落

首先得說明一下巴菲特為何需要知道股票股利複利利率。

巴菲特的想法中股票股利複利利率有2個意義：

• 一是代表管理階層提高每股盈餘的能力。
  計算過去十年和五年每股盈餘的年複利成長率，藉由了解長短期間的獲利年複利成長率，可以幫助我們了解一間公司長期的體質，並判斷管理階層的近程表現是否與長期表現一致。
  每股盈餘的增加，依公司運用保留盈餘的方式而定，長此以往，市場會因為每股盈餘的增加，而提高對股票的評價。
  
• 二是計算初期的投資報酬率。
  巴菲特利用股票股利複利利率得知某一檔股票目前的獲利複利利率，用以預測買入後的下次配股股利，以計算初期的投資報酬率，這個可以和公債的獲利利率比較，以決定買入的價格是否合適。
  

至於為何巴菲特計算出來的值較小？這是因為巴菲特注意的焦點在於期初的股利與期末股利所產生的複利趨勢，至於期間、與未來的變化則不是觀注的焦點，因為巴菲特相信：好股票是值得長期擁有的，至於短期間的股價變化，巴菲特則不在意。